A few people (Chris Drake, Tudor Timi, and anilraj) have already solved Sudoku using SystemVerilog. So, I am not the first one, but I can’t resist doing it because it sounds a lot of fun! I tried not to look at other people’s solutions and to code it easy-to-understand in mind. For those of you who don’t know about Sudoku, please see this.

Constraints

Solving Sudoku in SystemVerilog is nothing but specifying the rules with constraints. There are five constraints.

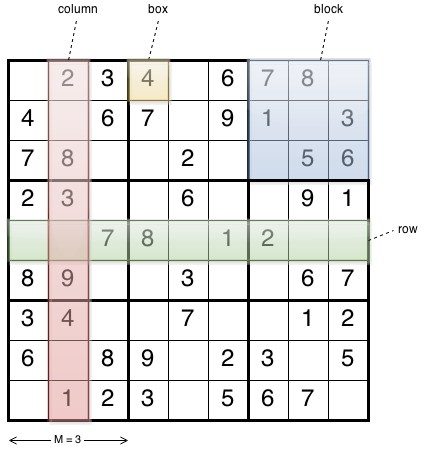
Box constraints

The value of each box must be between 1 and N, where N is M*M. See the figure above for the definition of M. For the typical 9×9 Sudoku, N is 9.

Row constraints

The boxes on the same row must have unique values.

Column constraints

The boxes on the same column must have unique values.

Block constraints

The boxes in the same MxM block must have unique values.

Puzzle constraints

A Sudoku puzzle to solve is given by an NxN array. The box must have the same value as the puzzle’s if the value is specified (zero represents a blank box). If the puzzle array has all-zero values, there are no puzzle constraints. In this case, a new Sudoku puzzle will be created.

Sudoku class

Here is the full list of the Sudoku class. See how the five constraints are defined in the class. The solve_this (line 64; note solve is a SystemVerilog keyword) is the main solver function. Simply randomizing this class will give us a solution (if it exists). The print function pretty-prints the solution.

class sudoku#( int M = 3 ); // M >= 1
  localparam N = M * M;
  local int unsigned puzzle[N][N];
  rand  int unsigned box   [N][N];
 
  // The value of each box must be between 1 and N.
 
  constraint box_con {
    foreach ( box[row, col] ) {
      box[row][col] inside { [ 1 : N ] };
    }
  }
 
  // The boxes on the same row must have unique values.
 
  constraint row_con {
    foreach   ( box[row, colA] ) {
      foreach ( box[   , colB] ) {
        if ( colA != colB ) { 
          box[row][colA] != box[row][colB];
        }
      }
    }
  }
 
  // The boxes on the same column must have unique values.
 
  constraint column_con {
    foreach   ( box[rowA, col] ) {
      foreach ( box[rowB,    ] ) {
        if ( rowA != rowB ) {
          box[rowA][col] != box[rowB][col];
        }
      }
    }
  }
 
  // The boxes in the same MxM block must have unique values.
 
  constraint block_con {
    foreach   ( box[rowA, colA] ) {
      foreach ( box[rowB, colB] ) {
        if ( rowA / M == rowB / M && 
             colA / M == colB / M && 
             ! ( rowA == rowB && colA == colB ) ) {
          box[rowA][colA] != box[rowB][colB];
        }
      }
    }
  }
 
  // The box must have the same value as the puzzle's if specified (!=0).
 
  constraint puzzle_con {
    foreach ( puzzle[row, col] ) {
      if ( puzzle[row][col] != 0 ) {
        box[row][col] == puzzle[row][col];
      }
    }
  }
 
  // Sudoku solver
 
  function int solve_this( int unsigned puzzle[N][N] );    this.puzzle = puzzle;
    return this.randomize();
  endfunction: solve_this
 
  // Print the solution.
 
  function void print();
    for ( int i = 0; i < N; i++ ) begin
      if ( i % M == 0 ) $write( "\n" );
      for ( int j = 0; j < N; j++ ) begin
        if ( j % M == 0 ) $write( " " );
        $write( "%3d", box[i][j] );
      end
      $write( "\n" );
    end
  endfunction: print
 
endclass: sudoku

Solving a puzzle

I created a sample puzzle shown below.

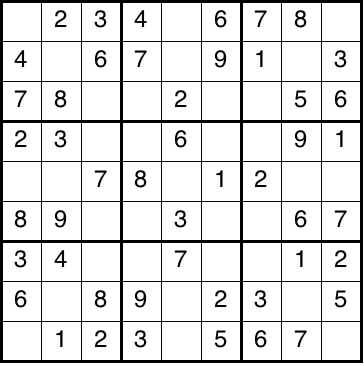
An array literal specifies the puzzle (line 8). Then, the top module calls the solve_this function (line 20).

module top;
  parameter  M = 3;
  localparam N = M * M;
  int unsigned puzzle[N][N];
  sudoku#( M ) s;
 
  initial begin
    puzzle = '{ '{ 0,2,3, 4,0,6, 7,8,0 }, // 0: blank box
                '{ 4,0,6, 7,0,9, 1,0,3 },
                '{ 7,8,0, 0,2,0, 0,5,6 },
 
                '{ 2,3,0, 0,6,0, 0,9,1 },
	        '{ 0,0,7, 8,0,1, 2,0,0 },
		'{ 8,9,0, 0,3,0, 0,6,7 },
 
                '{ 3,4,0, 0,7,0, 0,1,2 },
                '{ 6,0,8, 9,0,2, 3,0,5 },
                '{ 0,1,2, 3,0,5, 6,7,0 } };
    s = new;
    if ( s.solve_this( puzzle ) ) s.print();
    else $display( "cannot solve the puzzle" );
  end
endmodule: top

You should see the solution like this when you run.

   1  2  3   4  5  6   7  8  9
   4  5  6   7  8  9   1  2  3
   7  8  9   1  2  3   4  5  6
 
   2  3  4   5  6  7   8  9  1
   5  6  7   8  9  1   2  3  4
   8  9  1   2  3  4   5  6  7
 
   3  4  5   6  7  8   9  1  2
   6  7  8   9  1  2   3  4  5
   9  1  2   3  4  5   6  7  8

I hope this post won’t spoil fun of solving Sudoku 😉

You can view and run the code on EDA Playground (If M=3 takes too long to run, try M=2).

7 thoughts on “Hidden Gems of SystemVerilog – 3. Solving Sudoku”

Darshan Dehuniya says:

February 9, 2015 at 1:07 am

Nice Article,,,

Venkatesh Satrawada says:

March 4, 2016 at 11:46 am

Hi KK,
Never thought of sudoku using SV. This sounds fun. I am going to try this out myself and then go through your post.
Thanks, Venky

Huzefa Halolwala says:

May 12, 2016 at 3:15 am

I don’t understand the need of the constraint written in lines 40 to 50 in your code.If we remove that constraint then also the outcome is same.

1. Keisuke Shimizu says:
  
  May 21, 2016 at 2:52 pm
  Without block_con constraint, you might get an invalid solution like this:
```
   2  8  6   1  9  4   7  5  3
   6  2  7   9  5  3   4  1  8
   3  1  9   4  7  5   6  8  2

   9  6  8   3  2  7   5  4  1
   5  7  2   6  4  1   8  3  9
   1  9  4   8  3  6   2  7  5

   7  3  5   2  1  8   9  6  4
   8  4  1   5  6  9   3  2  7
   4  5  3   7  8  2   1  9  6
```
Sounderrajan Mohan says:

June 26, 2016 at 8:49 pm

Hi Keisuke, Really it sounds good!! I have never related SV constraints with solving sudoku. Finally SV helps me for non-technical thing. Thanks a lot for this article.

fu says:

December 18, 2016 at 7:58 am

how about use unique (in sv 2012) to solve this problem?can it work around?

1. Keisuke Shimizu says:
  
  January 29, 2017 at 6:34 pm
  
  Thanks for your suggestion. I wrote a new article to solve Sudoku using unique.